La médiane d'une D.O.1
Première convention
Selon la première convention, la médiane
 est l'observation occupant la
est l'observation occupant la
 -ème position dans la série statistique ordonnée (l'observation de rang
-ème position dans la série statistique ordonnée (l'observation de rang
 ).
).
Voyons, à partir de trois exemples légèrement différents, comment mettre en œuvre cette première convention lorsque les données sont présentées sous la forme d'une D.O.1.
Exemple : n est pair et un des effectifs cumulés de la D.O.1 est égal à n/2
Considérons la série statistique ordonnée de taille
 suivante :
suivante :

La médiane est
 .
.
Raisonnons à présent sur la D.O.1 associée à cette série statistique :

On s'aperçoit que la valeur 1, notre médiane, a pour caractéristique d'être la valeur observée à laquelle est associé un effectif cumulé égal à
 . On a donc ici exactement la moitié des observations avec des valeurs inférieures ou égales à la médiane et l'autre moitié des observations avec des valeurs strictement supérieures à la médiane.
. On a donc ici exactement la moitié des observations avec des valeurs inférieures ou égales à la médiane et l'autre moitié des observations avec des valeurs strictement supérieures à la médiane.
Exemple : n est pair et aucun des effectifs cumulés de la D.O.1 n'est égal à n/2
Considérons la série statistique ordonnée de taille
 suivante :
suivante :

La médiane est
 .
.
Raisonnons à présent sur la D.O.1 associée à cette série statistique :

Aucun des effectifs cumulés n'est égal à
 . Mais on s'aperçoit que la valeur
. Mais on s'aperçoit que la valeur
 , notre médiane, a pour caractéristique d'être la plus petite valeur observée dont l'effectif cumulé est supérieur à
, notre médiane, a pour caractéristique d'être la plus petite valeur observée dont l'effectif cumulé est supérieur à
 . On a ici un peu plus de la moitié des observations (6 observations parmi les 10) qui ont une valeur inférieure ou égale à la médiane.
. On a ici un peu plus de la moitié des observations (6 observations parmi les 10) qui ont une valeur inférieure ou égale à la médiane.
Exemple : n est impair
Considérons la série statistique ordonnée de taille
 suivante :
suivante :

La médiane est

Regardons à présent la D.O.1 associée à cette série statistique :

Aucun des effectifs cumulés n'est égal à
 Mais, à nouveau, la valeur
Mais, à nouveau, la valeur
 , notre médiane, a pour caractéristique d'être la plus petite valeur observée dont l'effectif cumulé est supérieur à
, notre médiane, a pour caractéristique d'être la plus petite valeur observée dont l'effectif cumulé est supérieur à

Méthode :
La détermination de la médiane d'une D.O.1 se fait à partir des effectifs cumulés associés aux valeurs distinctes observées :
s'il existe une valeur
 telle que
telle que
 , alors
, alors
 ;
;si aucun des effectifs cumulés n'est égal à
 , alors la médiane
, alors la médiane
 est égale à la plus petite valeur observée dont l'effectif cumulé est
est égale à la plus petite valeur observée dont l'effectif cumulé est
 ; en d'autres termes, la médiane
; en d'autres termes, la médiane
 est égale à la valeur
est égale à la valeur
 telle que
telle que
De manière plus synthétique, quelle que soit la D.O.1 rencontrée :
 est égale à la valeur
est égale à la valeur
 telle que
telle que
Ainsi, la médiane est la plus petite valeur observée dont l'effectif cumulé est supérieur ou égal à

Complément :
La médiane d'une D.O.1 peut tout aussi bien être déterminée à partir des fréquences cumulées associées aux valeurs distinctes observées :
 est égale à la valeur
est égale à la valeur
 telle que
telle que
En d'autres termes, la médiane est la plus petite valeur observée dont la fréquence cumulée est supérieure ou égale à

Seconde convention
Dans le cas où aucun des effectifs cumulés de la D.O.1 n'est égal à
 , la détermination de la médiane à partir de la D.O.1 se fait de la même manière avec les deux conventions : la médiane
, la détermination de la médiane à partir de la D.O.1 se fait de la même manière avec les deux conventions : la médiane
 est égale à la plus petite valeur observée dont l'effectif cumulé est supérieur à
est égale à la plus petite valeur observée dont l'effectif cumulé est supérieur à
 . Ce n'est donc que lorsqu'un des effectifs cumulés de la D.O.1 est égal à
. Ce n'est donc que lorsqu'un des effectifs cumulés de la D.O.1 est égal à
 que la seconde convention diffère de la première convention.
que la seconde convention diffère de la première convention.
Exemple : n est pair et un des effectifs cumulés de la D.O.1 est égal à n/2 (suite)
Considérons à nouveau la série statistique ordonnée de taille
 suivante :
suivante :

La médiane est

Raisonnons à présent sur la D.O.1 associée à cette série statistique :

 correspond à l'effectif cumulé associé à la valeur
correspond à l'effectif cumulé associé à la valeur
 . Dans ce cas, la médiane
. Dans ce cas, la médiane
 coïncide avec la moyenne de cette valeur
coïncide avec la moyenne de cette valeur
 et de la valeur
et de la valeur
 qui la suit.
qui la suit.
Méthode :
La détermination de la médiane d'une D.O.1 se fait à partir des effectifs cumulés ou des fréquences cumulées associé(e)s aux valeurs distinctes observées :
si aucun des effectifs cumulés n'est égal à
 (ou si aucune des fréquences cumulées n'est égale à
(ou si aucune des fréquences cumulées n'est égale à
 ), alors la médiane
), alors la médiane
 est égale à la valeur
est égale à la valeur
 telle que
telle que
 (en posant
(en posant
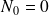 si
si
 ) ou encore, de manière équivalente, si
) ou encore, de manière équivalente, si
 (en posant
(en posant
 si
si
 ) ;
) ;s'il existe une valeur
 telle que
telle que
 (
(
 ), alors
), alors













